您现在的位置是: 首页 > 热门专业 热门专业
柯西不等式与高考,柯西不等式高考考吗
tamoadmin 2024-05-22 人已围观
简介内容如下:1、二维形式:(a^2+b^2)(c^2 + d^2)(ac+bd)^2。2、三角形式:(a^2+b^2)+(c^2+d^2)[(a-c)^2+(b-d)^2]。3、向量形式:|α||β||α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n2)。4、一般形式:(∑ai^2)(∑bi^2) (∑ai·bi)^2。常用定理:①不等式F(x)< G(x)与
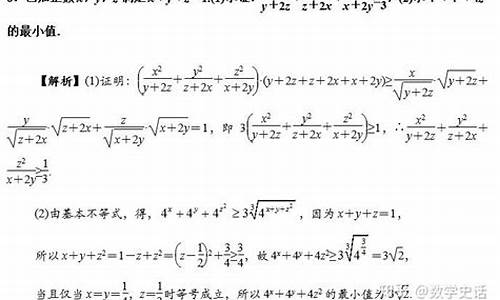
内容如下:
1、二维形式:(a^2+b^2)(c^2 + d^2)≥(ac+bd)^2。
2、三角形式:√(a^2+b^2)+√(c^2+d^2)≥√[(a-c)^2+(b-d)^2]。
3、向量形式:|α||β|≥|α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n≥2)。
4、一般形式:(∑ai^2)(∑bi^2) ≥ (∑ai·bi)^2。
常用定理:
①不等式F(x)< G(x)与不等式 G(x)>F(x)同解。
②如果不等式F(x) < G(x)的定义域被解析式H( x )的定义域所包含,那么不等式 F(x)<G(x)与不等式F(x)+H(x)<G(x)+H(x)同解。
③如果不等式F(x)<G(x) 的定义域被解析式H(x)的定义域所包含,并且H(x)>0,那么不等式F(x)<G(x)与不等式H(x)F(x)<H( x )G(x) 同解。
④不等式F(x)G(x)>0与不等式同解;不等式F(x)G(x)<0与不等式同解。
1、二维形式:(a^2+b^2)(c^2 + d^2)≥(ac+bd)^2
2、三角形式:√(a^2+b^2)+√(c^2+d^2)≥√[(a-c)^2+(b-d)^2]
3、向量形式:|α||β|≥|α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n≥2)
4、一般形式:(∑ai^2)(∑bi^2) ≥ (∑ai·bi)^2
扩展资料:
①如果x>y,那么y<x;如果y<x,那么x>y;(对称性)
②如果x>y,y>z;那么x>z;(传递性)
③如果x>y,而z为任意实数或整式,那么x+z>y+z;(加法原则,或叫同向不等式可加性)
④ 如果x>y,z>0,那么xz>yz;如果x>y,z<0,那么xz<yz;(乘法原则)
百度百科-不等式