您现在的位置是: 首页 > 热门院校 热门院校
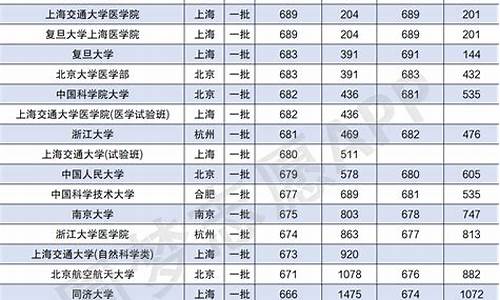
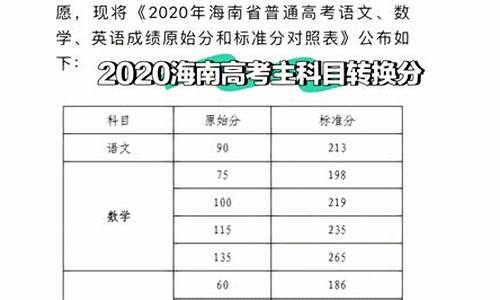
高考数学理科甲卷_高考数学1理
tamoadmin 2024-05-14 人已围观
简介!是解答题的3吗?!!有的显示不出出来,可以发邮箱给我,我把word发给你!3、(12分) 解法一:(1)连结BD,取DC的中点G,连结BG, 由此知DG=GC=BG=1,即△DBC为直角三角形,故BCBD.又SD平面ABCD,故BCSD,所以BC平面BDS,BCDE.作BKEC,K为垂足.因平面EDC平面SBC,故BK平面EDC,BKDE.DE与平面SBC内的两条相交直线BK、BC都垂直,DE平

!是解答题的3吗?!!有的显示不出出来,可以发邮箱给我,我把word发给你!
3、(12分) 解法一:(1)连结BD,取DC的中点G,连结BG,
由此知DG=GC=BG=1,即△DBC为直角三角形,故BC⊥BD.
又SD⊥平面ABCD,故BC⊥SD,
所以BC⊥平面BDS,BC⊥DE.
作BK⊥EC,K为垂足.因平面EDC⊥平面SBC,故BK⊥平面EDC,BK⊥DE.DE与平面SBC内的两条相交直线BK、BC都垂直,
DE⊥平面SBC,DE⊥EC,DE⊥SB.
SB= = ,
DE= = ,
EB= = ,SE=SB-EB= ,
所以SE=2EB.
(2)由SA= = ,AB=1,SE=2EB,AB⊥SA,知AE= =1,又AD=1,
故△ADE为等腰三角形.
取ED中点F,连结AF,则AF⊥DE,AF= = .
连结FG,则FG∥EC,FG⊥DE.
所以∠AFG是二面角A—DE—C的平面角.
连结AG,AG= ,FG= = ,
cos∠AFG= =- .
所以二面角A-DE-C的大小为120°.
解法二:以D为坐标原点,射线DA为x轴正半轴,建立如图所示的直角坐标系Dxyz.
设A(1,0,0),则B(1,1,0),C(0,2,0),S(0,0,2).
(1) =(0,2,-2),
=(-1,1,0).
设平面SBC的法向量为
n=(a,b,c),
由n⊥ ,n⊥ 得n? =0,n? =0.
故2b-2c=0,-a+b=0.
令a=1,则b=1,c=1,n=(1,1,1).
又设 =λ (λ>0),
则E( , , ).
=( , ,), =(0,2,0).
设平面CDE的法向量m=(x,y,z),
由m⊥ ,m⊥ ,得
m? =0,m? =0.
故 + + =0,2y=0.
令x=2,则m=(2,0,-λ).
由平面DEC⊥平面SBC得m⊥n,m?n=0,2-λ=0,λ=2.
故SE=2EB.
(2)由(1)知E( , , ),取DE中点F,则F( , , ), =( ,- ,- ),
故 ? =0,由此得FA⊥DE.
又 =(- , ,- ),故 ? =0,由此得EC⊥DE,
向量与的夹角等于二面角ADEC的平面角.
于是cos〈 , 〉= =- ,
所以二面角A-DE-C的大小为120°